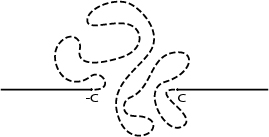The moving needle problem

ConanLeave a comment

First, let’s clarify that this post has nothing to do with the Kakeya conjecture (except for the word ‘needle’ in it). Anyways, I was asked the following question via an e-mail from Charles this summer: (It turns out that the question was invented by Jonathan King and then communicated to Morris Hirsch and that’s where Charles heard about it from) In any case, I find the problem quite cute:

Problem: Given a smoothly embedded copy of \mathbb{R} in \mathbb{R}^3 containing \{ (x,0,0) \ | \ x \in (-\infty,-C] \cup [C, \infty) \}. Is it always possible to continuously slide a unit length needle lying on the ray (-\infty, -C] to the ray [C, \infty), while keeping the head and tail of the needle on the curve throughout the process?

i.e. the curve is straight once it passes the point (-C, 0) and (C,0), but can be bad between the two points:

We are interested in sliding the needle from the neigative x-axis to the positive x-axis:

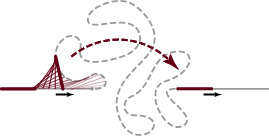
Exercise: Try a few examples! It’s quite amusing to see that sometimes both ends of the needle needs to go back and forth along the curve many times, yet it always seem to get through.

One should note that this is not possible if we just require the curve to be eventually straight and goes to infinity at both ends. As we can see on a simple ‘hair clip’ curve:

The curve consists of two parallel rays of distance <1 apart, connected with a semicircle. A unit needle can never get from one ray to the other since the needle would have to rotate 180 degrees and hence it has to be vertical at some point in the process, but no two points on the curve has vertical distance 1.

After some thought, I think I can show for each given curve, 'generic' needle length can pass through:

Claim: For any C^2 embedding as above, there is a full measure and dense G_\delta set \mathcal{L} \subseteq \mathbb{R} of lengths where the needle of any length L \in \mathcal{L} can slide through the curve.

Proof: Let \gamma: \mathbb{R} \rightarrow \mathbb{R}^3 be a smooth parametrization of the curve s.t. \gamma(t) = t for t \in (-\infty, -C] \cup [C, \infty).

Define \varphi: \mathbb{R}^2 \rightarrow \mathbb{R} where \varphi: (s, t) \mapsto d(\gamma(s), \gamma(t)).

Hence \varphi vanishes on the diagonal and takes positive value everywhere else.
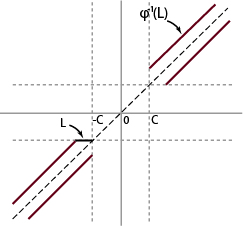
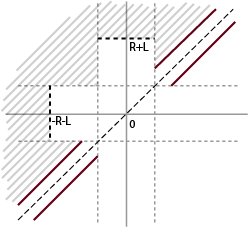
Since \gamma(t) = t for t \notin (-C, C), hence \varphi(s,t)=|s-t| for |s|, |t|>C. \varphi^{-1}(L) contains four rays \{ |s-t| = L \ | \ s, t \notin (-C, C) \}:

Observation: a needle of length L can slide through the curve iff there is a continuous path in the level set \varphi(p) = L connecting the two rays above the diagonal. (This is merely projection onto the x and $larex y$-axis.)

We also have \varphi is C^2 other than on the diagonal. (It behaves like the absolute value function near the diagonal). By Sard’s theorem, since \varphi is C^2 on \{s < t\}, the set of critical values is both measure 0 and first category.

Let \mathcal{L} be the set of regular values of \varphi. For any L \in \mathcal{L}, by implicit function theorem, the level set \varphi^{-1}(L) is a C^2 sub-manifold.

Since the arc \gamma([-C, C]) is compact, we can find large R where \gamma([-C, C]) \subseteq B(\bar{0}, R).

Hence for |t| > R + L and s \in [-C, C], we have

\varphi (s, t) = d(\gamma(s), \gamma(t)) > d(\gamma(t), B(\bar{0}, R)) > L

The same holds with |s| > R + L and t \in [-C, C]

i.e. \varphi takes value >L in the shaded region below:

Hence for L \in \mathcal{L}, \varphi^{-1}(L) \cap \{x \leq y\} is a 1 dimensional sub-manifold, outside a bounded region it contains only two rays. We also know that the level set is bounded away from the diagonal since \varphi vanishes on the diagonal. By an non-ending arc argument, one connected component of \varphi^{-1}(L) must be a curve connecting the end points of the two rays. Establishes the claim.

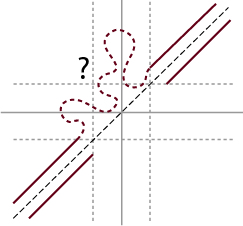
Remarks: This problem happens to come up at the very end (questio/answer part) of Charles’s talk in the midwest dynamics conference last month (where he talked about our joint work about funnel sections). A couple weeks later Michal Misiurewicz e-mailed us a counter-example when the curve is not smooth (only continuous).

Initially I tried to use the above argument to get the length 1 needle. Everything works fine until a point where one has a continuum in the level set connecting the end-points of the two rays. We want the continuum to be path connected. I got stuck on that. In the continuous curve case, Michal’s counter-example corresponds to the continuum containing a \sin(1/x) curve, hence is not path connected.

I believe such thing cannot happen for smooth. The hope would be that the length 1 needle can slide through any C^2 (or C^1) curve. (Note that once the length 1 needle can pass through, then all length can pass through just by rescaling the curve.) In any case, still trying…

Leave a comment